------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
현재 보고있는 강의는 구버전입니다. 내용에는 문제가 없으나 리뉴얼 중이니 이 게시글을 참고해주세요.
리뉴얼한 버전은 [실전 알고리즘] 0x1C강 - 플로이드 알고리즘에서 확인할 수 있습니다. 리뉴얼 버전으로 보시는 것을 추천드립니다
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

안녕하세요, 오늘은 플로이드 알고리즘을 다루겠습니다. 이제 최단경로 알고리즘인 플로이드, 다익스트라 알고리즘만 끝내고 나면 드디어 실전 알고리즘 강의도 끝이 나네요. 이 강의를 보는 여러분 모두 화이팅입니다.

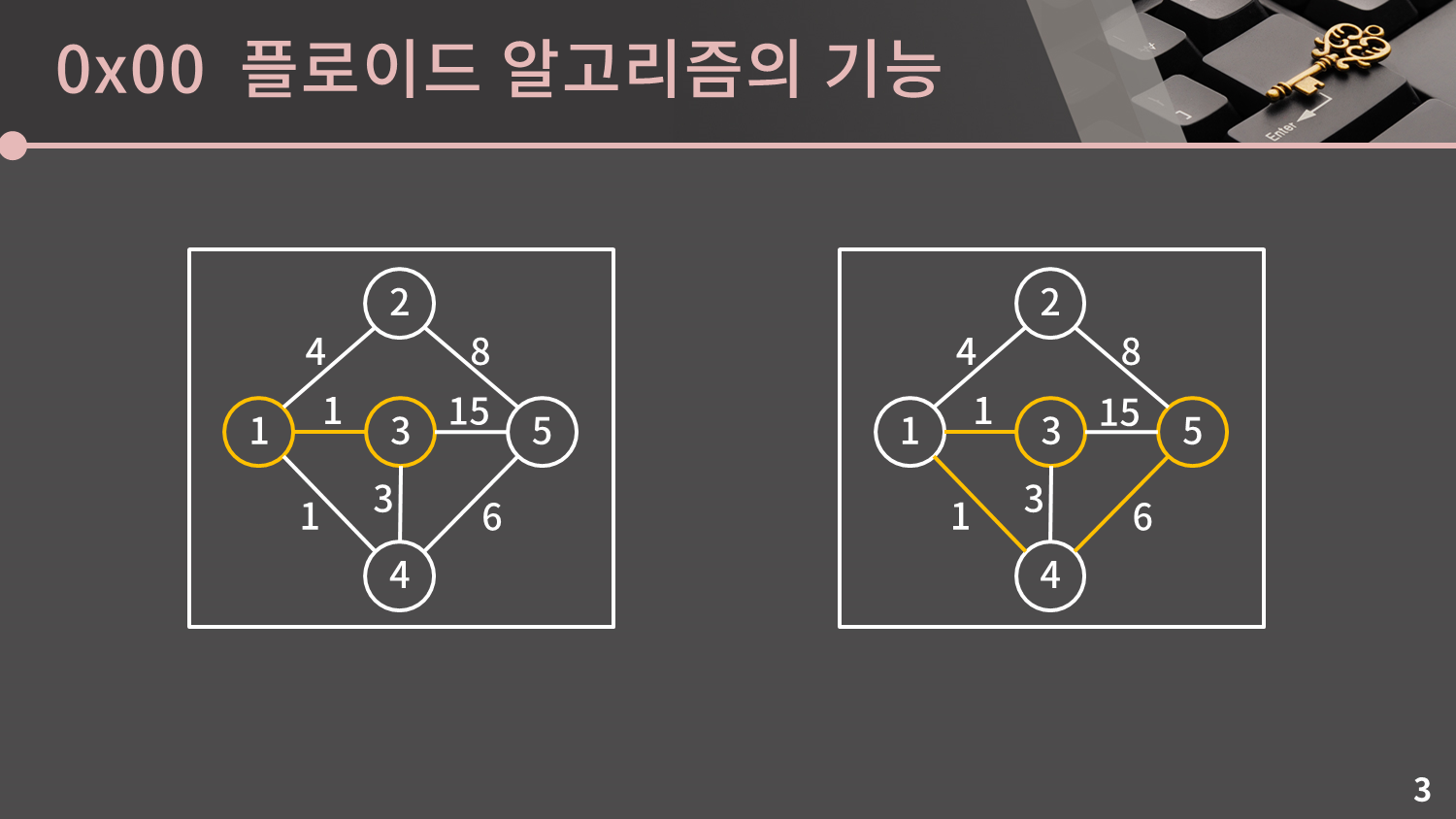
우리는 이미 직관적으로 그래프에서의 최단 거리라는 개념을 알고 있지만 그래도 한 번 짚고 넘어가겠습니다.
그래프를 예쁘게 잘 만들어놓은 것 같아 다시 재활용했습니다. 주어진 그래프에서 간선 옆에 적힌 값들이 간선의 거리를 의미합니다. 혹은 비용이라고 부르기도 합니다. 아무튼 이런 상황에서 1에서 3으로 가는 최단 거리는 1입니다. 3에서 5로 가는 최단 거리는 8입니다. 15인 간선을 활용하는 것 보다 돌아가는 것이 이득이기 때문입니다.

플로이드 알고리즘은 오른쪽 테이블과 같이 주어진 그래프에서 모든 정점 쌍 사이의 최단 거리를 구해주는 알고리즘입니다. 주어진 그래프는 무방향 그래프이지만 그래프가 방향 그래프이건, 무방향 그래프이건 상관이 없습니다. 단, 간선의 합이 음수인 사이클이 있다면 문제가 생기는데 애초에 간선의 값이 음수인 상황이 딱히 일반적이지 않으니 당장은 고민하지 맙시다.
이전에 관련 내용을 다룬 적이 없다면 도대체 어떻게 주어진 그래프에서 임의의 시작점으로부터 임의의 도착점까지의 최단 거리를 모두 구할 수 있는지 막막할 것입니다. 관련 내용을 배운 적이 없음에도 불구하고 방법이 쉽게 떠오른다면 코딩테스트를 준비할게 아니라 대학원에 진학하셔서 우리나라를 빛내주세요ㅎㅎ..
다행히 플로이드 알고리즘은 구현이 아주 쉬운 편에 속합니다. 그렇기에 이전 강에서 고통받았다면 이번에는 조금이나마 더 편한 마음으로 강의를 들을 수 있지 않을까 싶습니다.
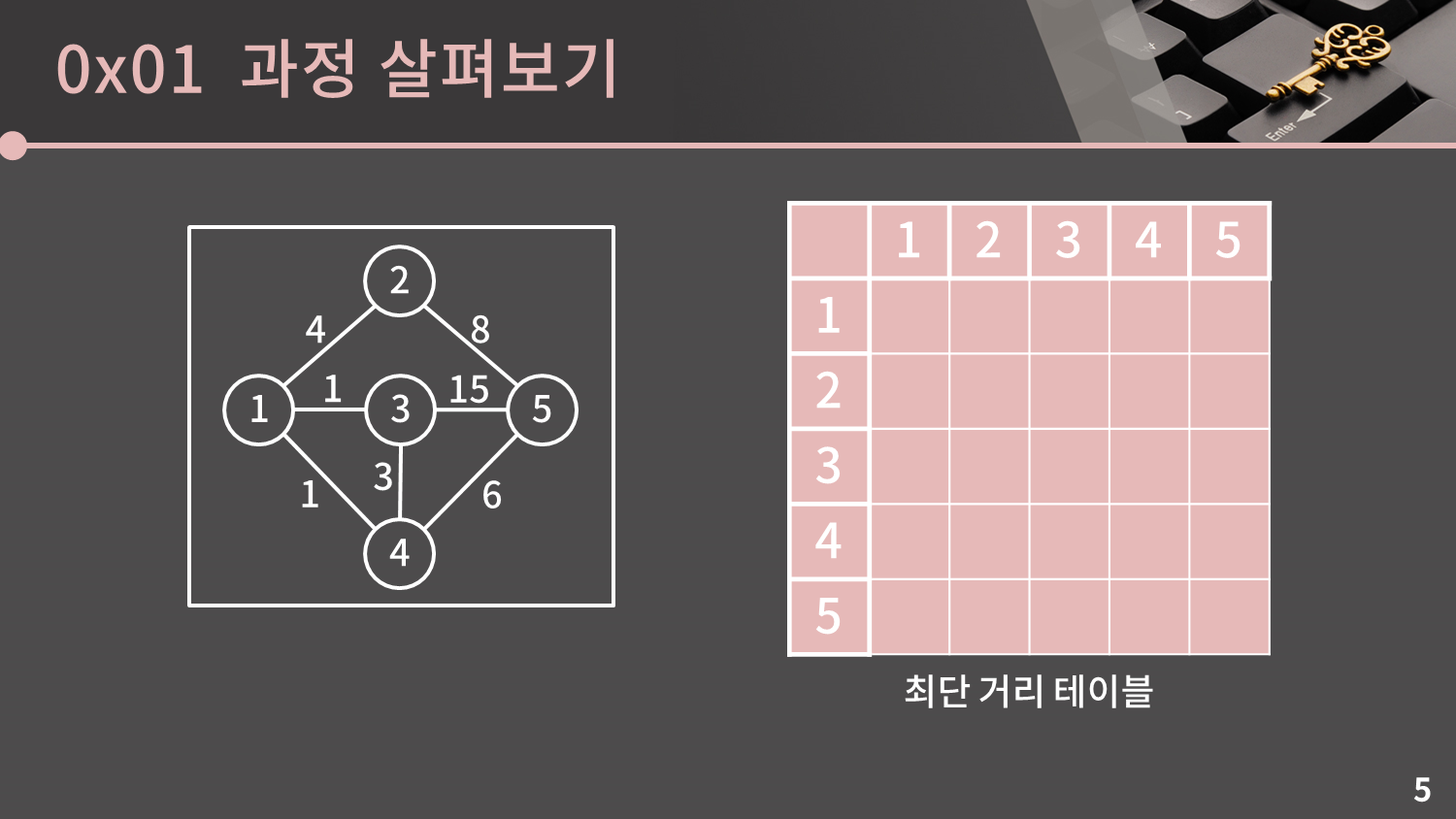
이제 플로이드 알고리즘의 과정을 알아보겠습니다. 설명을 돕기 위해 그래프와 빈 테이블을 모셔왔습니다.

일단 테이블에서 당장 채울 수 있는 것만 채워보겠습니다. 자기 자신으로 가는 거리는 당연히 0이고, 또 간선 1개로 바로 건너갈 수 있는 곳 또한 간선의 값으로 바로 채워질 것입니다. 지금은 그래프가 무방향 그래프이기 때문에 (1, 2)와 (2, 1)이 모두 4로 채워졌지만 만약 방향 그래프였다면 하나만 채워졌을 것입니다.
그래프에 간선이 많기 때문에 자명한 것들만 채워도 꽤 많이 채워지긴 했습니다. 하지만 이 값은 여러 문제가 있습니다. 예를 들어 3에서 5로 가는 최단 거리가 8인데 지금은 간선 1개 짜리만 보니 15로 채워져있네요. 그리고 1에서 5로 가는 최단 거리는 아예 알아내지도 못해 ∞이 들어있습니다. 아직 테이블은 고쳐야할게 많습니다.
이제 여기서 플로이드 알고리즘은 아주 훌륭한 접근법을 생각해냅니다.
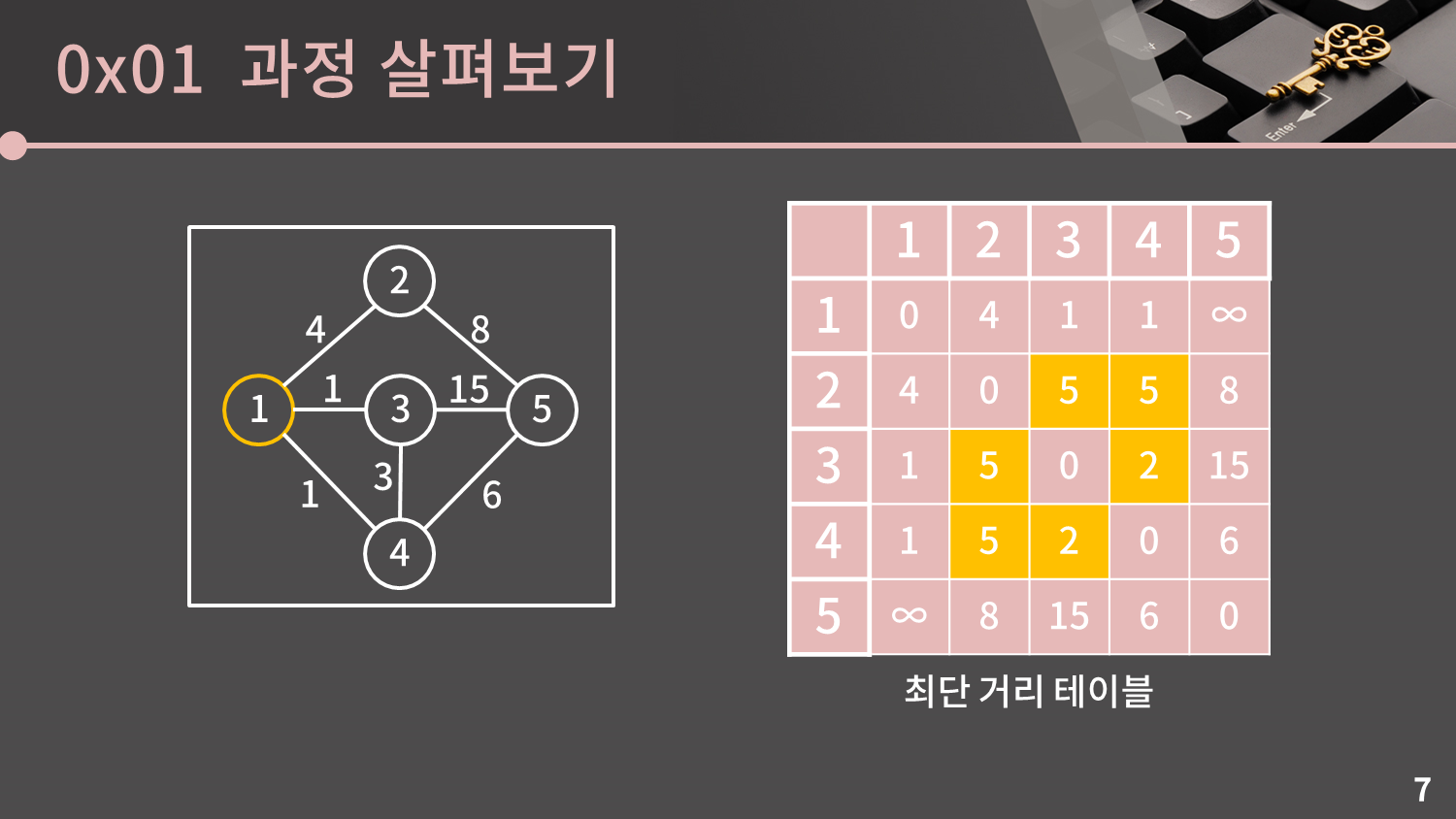
그 접근법이란, 바로 현재 테이블에서 일단 1번을 거쳐가는 최단 거리만을 먼저 갱신하는 것입니다.
현재 테이블에 적힌 값을 "불완전한 최단 거리"으로 생각하지 말고, "중간에 다른 정점을 거치지 않았을 때의 최단 거리"이라고 생각하면 조금 더 이해에 도움이 될 것 같습니다.
이제 "중간에 다른 정점을 거치지 않았을 때의 최단 거리"가 저장되어있던 테이블을 "중간에 다른 정점을 거치지 않았거나 1번 정점을 거쳐서 갈 때의 최단 거리"가 저장되도록 수정할 것입니다.
즉, 현재는 2에서 4로 가는 거리가 ∞인데 1을 거쳐서 가면 2에서 1로 가는 간선, 1에서 4로 가는 간선을 이용해 거리 5로 갈 수가 있게 됩니다.
해당 테이블을 $D$라고 합시다. $s$에서 $t$로 갈 때 1번 정점을 거쳐가는 최단 거리는 $D[s][1] + D[1][t]$입니다. $D[s][1] + D[1][t]$가 의미하는 바는 $s$에서 1까지 최단 경로로 가고, 그 후 1부터 $t$까지 다시 최단 경로로 갔을 때의 값이기 때문입니다. 만약 $D[s][t]$보다 $D[s][1] + D[1][t]$가 작을 경우, 즉 1번 정점을 거쳐가는 것이 효율적일 때에만 $D[s][t]$를 $D[s][1] + D[1][t]$로 갱신해주면 됩니다.
주어진 테이블에서는 $D[2][3], D[2][4], D[3][2], D[3][4], D[4][2], D[4][3]$이 갱신됩니다.

현재 테이블에 적힌 값은 "중간에 다른 정점을 거치지 않았거나 1번 정점을 거쳐서 갈 때의 최단 거리"입니다. 이것을 "중간에 다른 정점을 거치지 않았거나 1, 2번 정점을 거쳐서 갈 때의 최단 거리"로 수정할 것입니다.
방법은 이전과 마찬가지입니다. 비슷한 논리로 생각했을 때 $s$에서 $t$로 갈 때 2번 정점을 거쳐가는 최단 거리는 $D[s][2] + D[2][t]$입니다. 만약 $D[s][t]$보다 $D[s][2] + D[2][t]$가 작을 경우 $D[s][t]$를 $D[s][2] + D[2][t]$로 갱신해주면 됩니다.
주어진 테이블에서는 $D[1][5], D[3][5], D[5][1], D[5][3]$이 갱신됩니다.
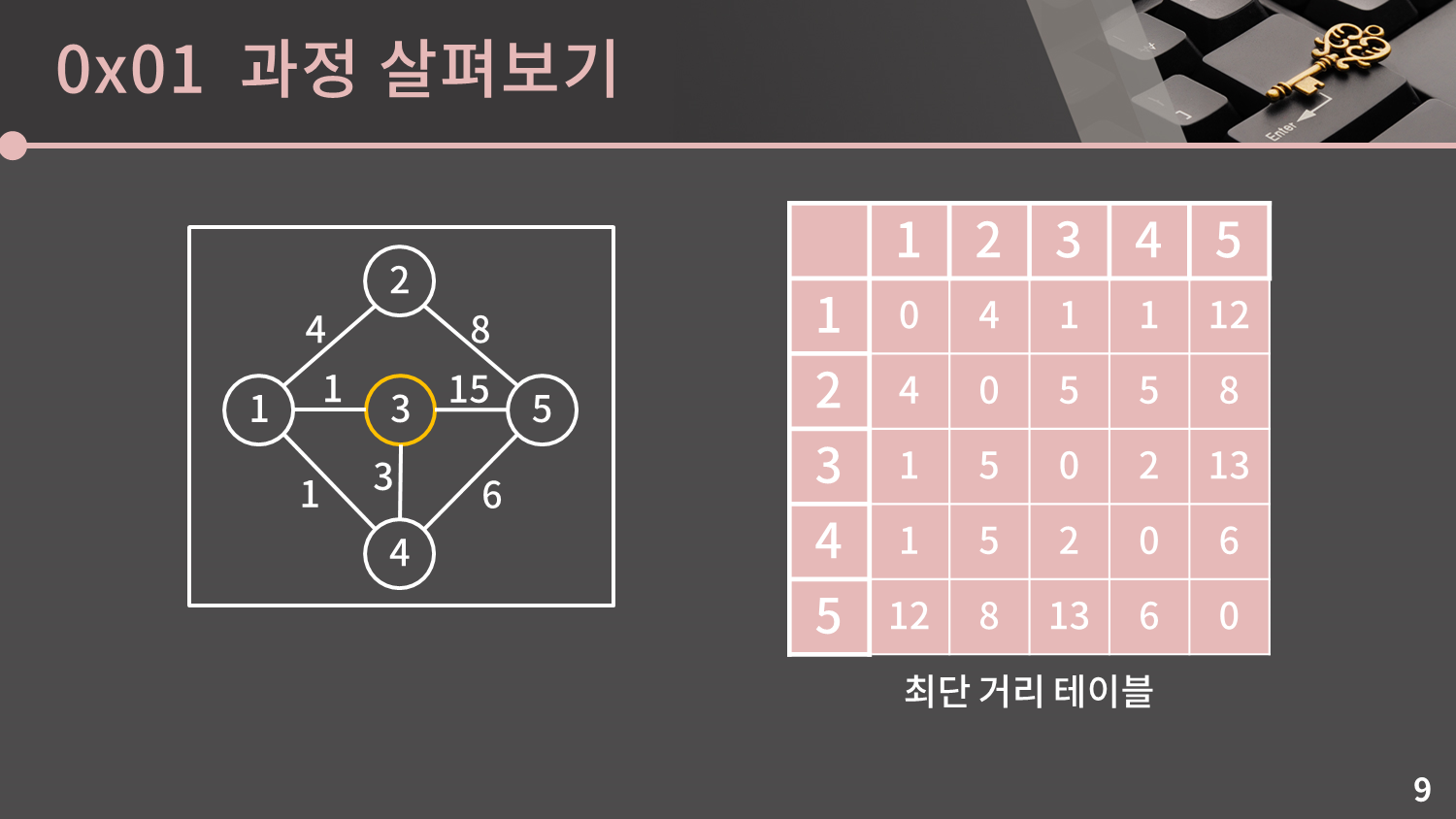
이제 대충 느낌이 오시나요? 현재 테이블에 적힌 값은 "중간에 다른 정점을 거치지 않았거나 1, 2번 정점을 거쳐서 갈 때의 최단 거리"입니다. 이것을 "중간에 다른 정점을 거치지 않았거나 1, 2, 3번 정점을 거쳐서 갈 때의 최단 거리", "중간에 다른 정점을 거치지 않았거나 1, 2, 3, 4번 정점을 거쳐서 갈 때의 최단 거리", 마지막으로 "중간에 다른 정점을 거치지 않았거나 1, 2, 3, 4, 5번 정점을 거쳐서 갈 때의 최단 거리 = 최종적인 최단 거리"까지 쭉쭉 나아가면 됩니다.
테이블에 3번을 거쳐가는 최단 거리를 반영합시다. $D[s][t]$보다 $D[s][3] + D[3][t]$가 작을 경우 $D[s][t]$를 $D[s][3] + D[3][t]$로 갱신해주면 됩니다.
$D[s][t]$보다 $D[s][3] + D[3][t]$가 작은 경우가 없어 주어진 테이블에서는 아무 값도 변경되지 않습니다.
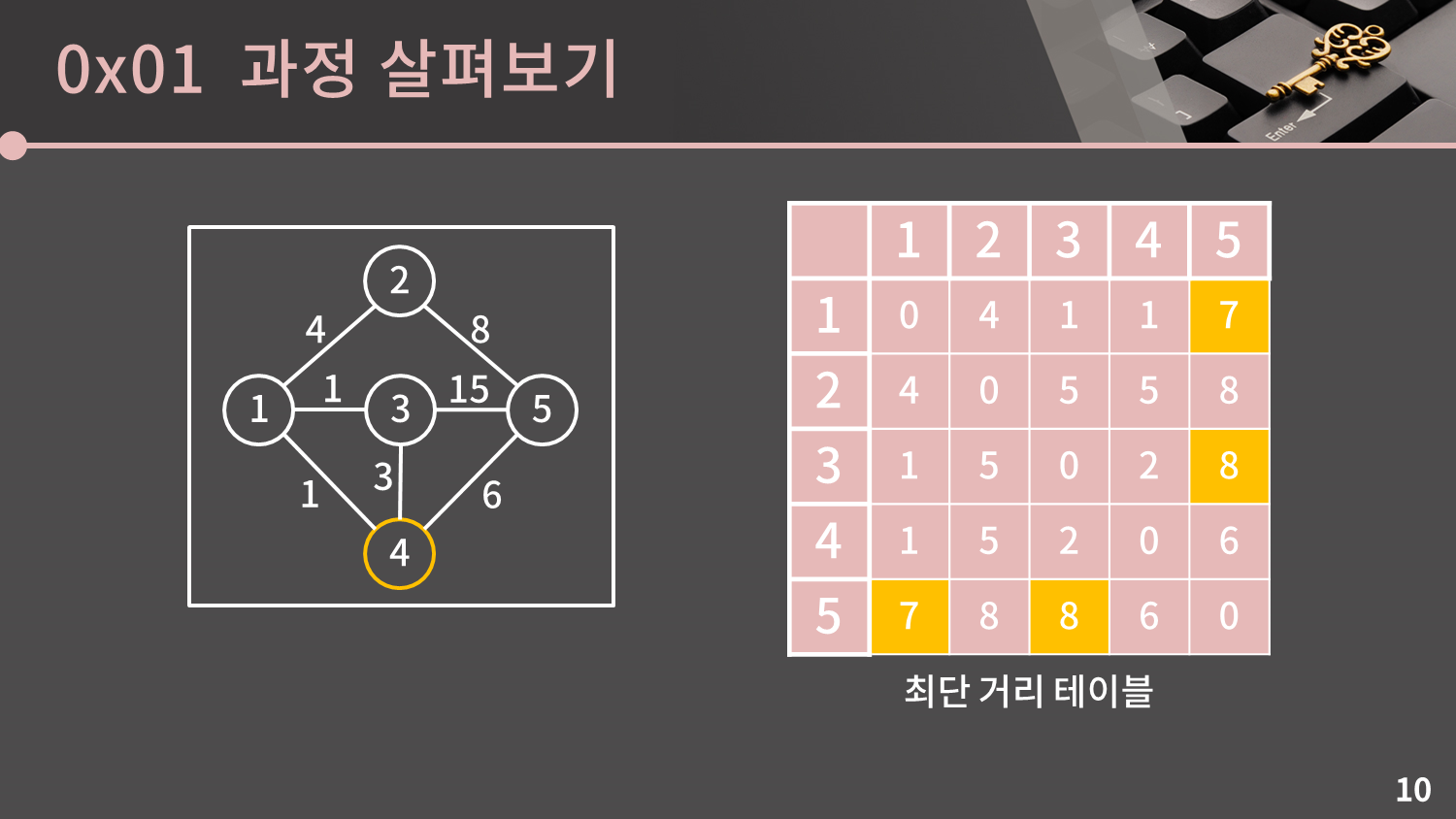
테이블에 4번을 거쳐가는 최단 거리를 반영합시다. $D[s][t]$보다 $D[s][4] + D[4][t]$가 작을 경우 $D[s][t]$를 $D[s][4] + D[4][t]$로 갱신해주면 됩니다.
주어진 테이블에서는 $D[1][5], D[3][5], D[5][1], D[5][3]$이 갱신됩니다.
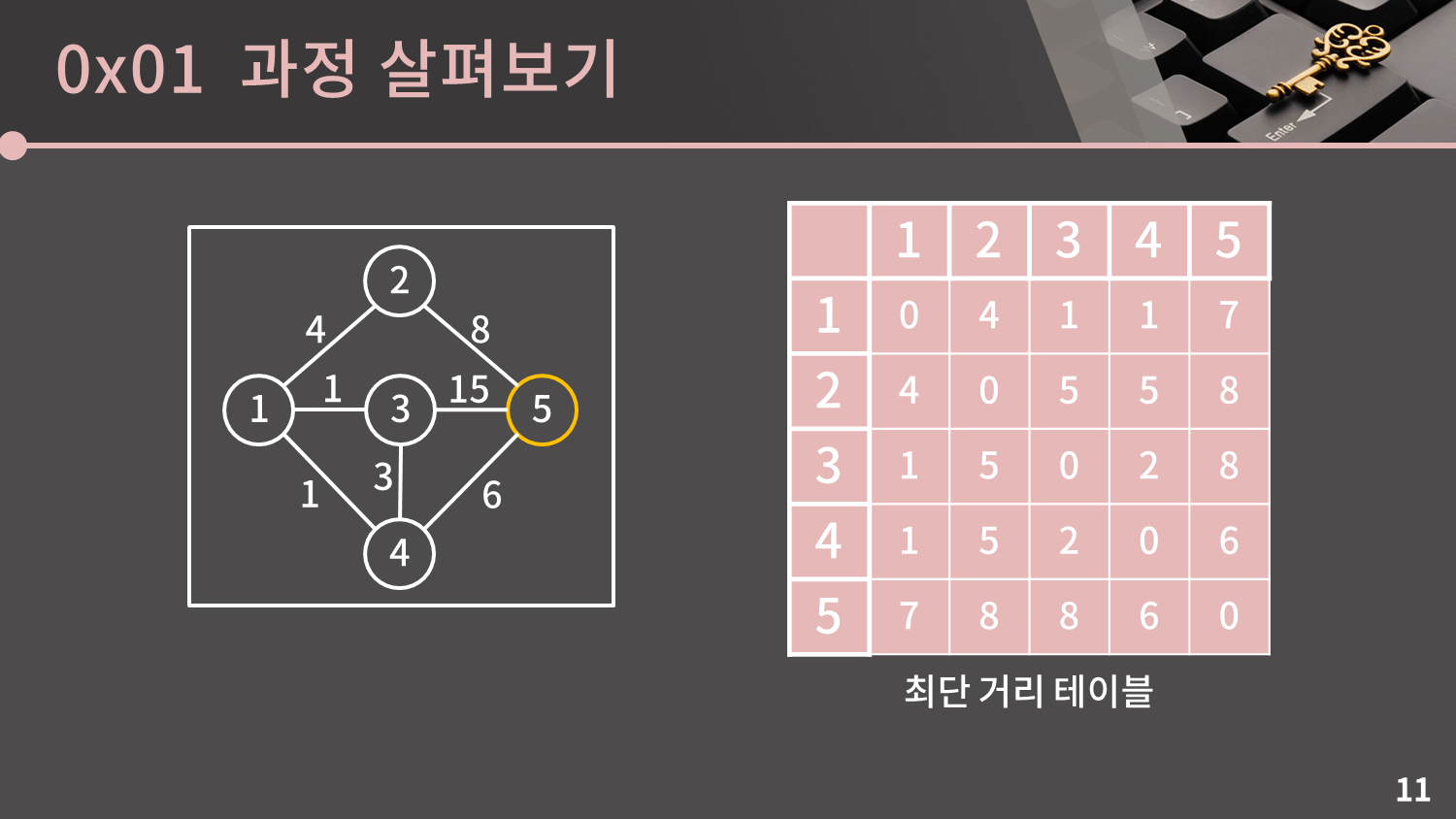
마지막으로 테이블에 5번을 거쳐가는 최단 거리를 반영합시다. $D[s][t]$보다 $D[s][5] + D[5][t]$가 작을 경우 $D[s][t]$를 $D[s][5] + D[5][t]$로 갱신해주면 됩니다.
$D[s][t]$보다 $D[s][5] + D[5][t]$가 작은 경우가 없어 주어진 테이블에서는 아무 값도 변경되지 않습니다.
이렇게 플로이드 알고리즘이 종료되었습니다. 정점이 $V$개라고 할 때 총 $V$단계에 걸쳐 갱신이 이루어지고 각 $k=1,2,3,\dots,V$단계마다 총 $V^2$개의 모든 $D[s][t]$값을 $D[s][k]+D[k][t]$값과 비교하므로 플로이드 알고리즘의 시간복잡도는 $O(V^3)$입니다.
지금 다룬 플로이드 알고리즘이 반드시 최단거리를 반환한다는 것을 저희는 다소 두리뭉실하게 다루었습니다. 알고리즘의 정당성을 귀납법을 이용해 수학적으로 엄밀하게 증명할 수 있지만 생략하도록 하겠습니다.

구현은 정말정말정말정말정말 쉽습니다. for문 3개를 통해 테이블을 갱신해주기만 하면 됩니다. BOJ 11404번: 플로이드 문제는 무방향 그래프에서 최단 거리들을 구하는 문제입니다. 정답 코드를 살펴봅시다. 물론 그 전에 가능하면 직접 한 번 풀어보시면 좋겠고, 다음 슬라이드부터는 정답 코드를 놓고 분석할 예정이라 충분히 혼자 시도해본 후에 다음 슬라이드로 넘어와주세요.

일단 거리가 무한인 것을 나타내기 위한 INF 값은 10억+10으로 잡았습니다. 어느 두 도시의 최단 거리가 아무리 커봤자 $99 \times 100,000$ 이기에 이 값보다 큰 값을 INF로 삼으면 되지만 INF값 2개를 더했을 때 int overflow가 나지 않게 조심해야합니다. 예를 들어 INF를 0x7f7f7f7f 으로 뒀을 경우에는 22번 줄에서 int overflow가 발생할 것입니다.
11번 줄부터 18번 줄까지는 입력을 받고 d 테이블을 채우는 루틴입니다. 일단 모든 행렬값을 INF로 둔 후, a, b, c가 주어지면 d[a][b]를 갱신합니다. 그런데 단순히 $d[a][b] = c$ 로 두는 것이 아니라 왜 17번 줄과 같이 썼을까요? 왜냐하면 문제에서 시작 도시와 도착 도시를 연결하는 노선은 하나가 아닐 수 있다 라는 단서를 주었기 때문입니다. 1번에서 2번 도시로 가는 노선이 비용 3짜리도 있고 4짜리도 있을 때 $d[1][2]$를 3으로 두어야 하기 때문입니다.
이후 19~22번 줄에서 d 테이블을 갱신해준 후 출력을 함으로서 문제를 해결할 수 있게 됩니다.
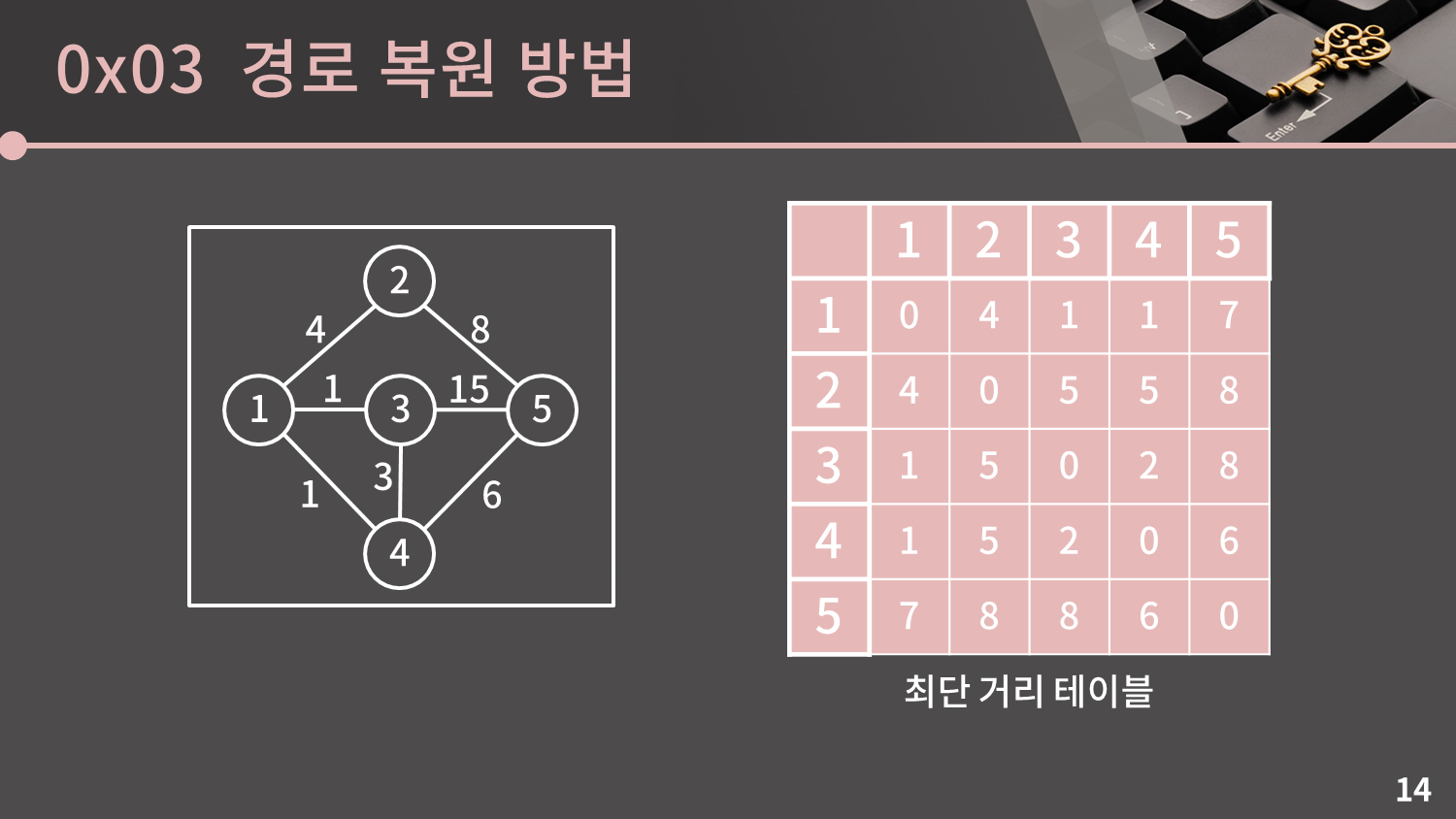
플로이드 알고리즘을 통해 우리는 주어진 그래프에서 임의의 시작점으로부터 임의의 도착점까지의 최단 거리를 알 수 있게 되었습니다. 그런데 지금은 거리만 알고 있을 뿐 최단 거리로 가기 위해서 실제 어떤 경로로 가야하는지는 전혀 알지 못합니다.
예를 들어 3에서 5로 가는 최단 거리가 8인건 알겠는데, 3->1->4->5로 가야한다는 사실을 알 수 없다는 뜻입니다.
그래서 이번 챕터에서는 플로이드 알고리즘에서 어떻게 경로 복원을 할 수 있는지 다뤄보도록 하겠습니다.

$a$에서 $b$까지 최단 거리로 가는 전체 경로를 다 복원하려고 들지 말고 딱 한 단계만 해봅시다. $a$에서 $b$까지 최단 거리로 가려면 $a$에서 어느 정점으로 가야 하는지만 생각해봅시다. 이를 $nxt$ 테이블이라고 부르겠습니다.
일단 최단 거리 테이블과 nxt 테이블을 모두 비워뒀습니다.

"중간에 다른 정점을 거치지 않았을 때의 최단 거리"를 먼저 채워보겠습니다. $nxt$ 테이블도 지금까지는 큰 어려움 없이 채울 수 있는데, 예를 들어 1에서 2로 가는 간선이 있으므로 $nxt[1][2]$는 2가 됩니다. 1에서 2까지 가려고 1에서 출발했다면 바로 2로 가면 되기 때문입니다.
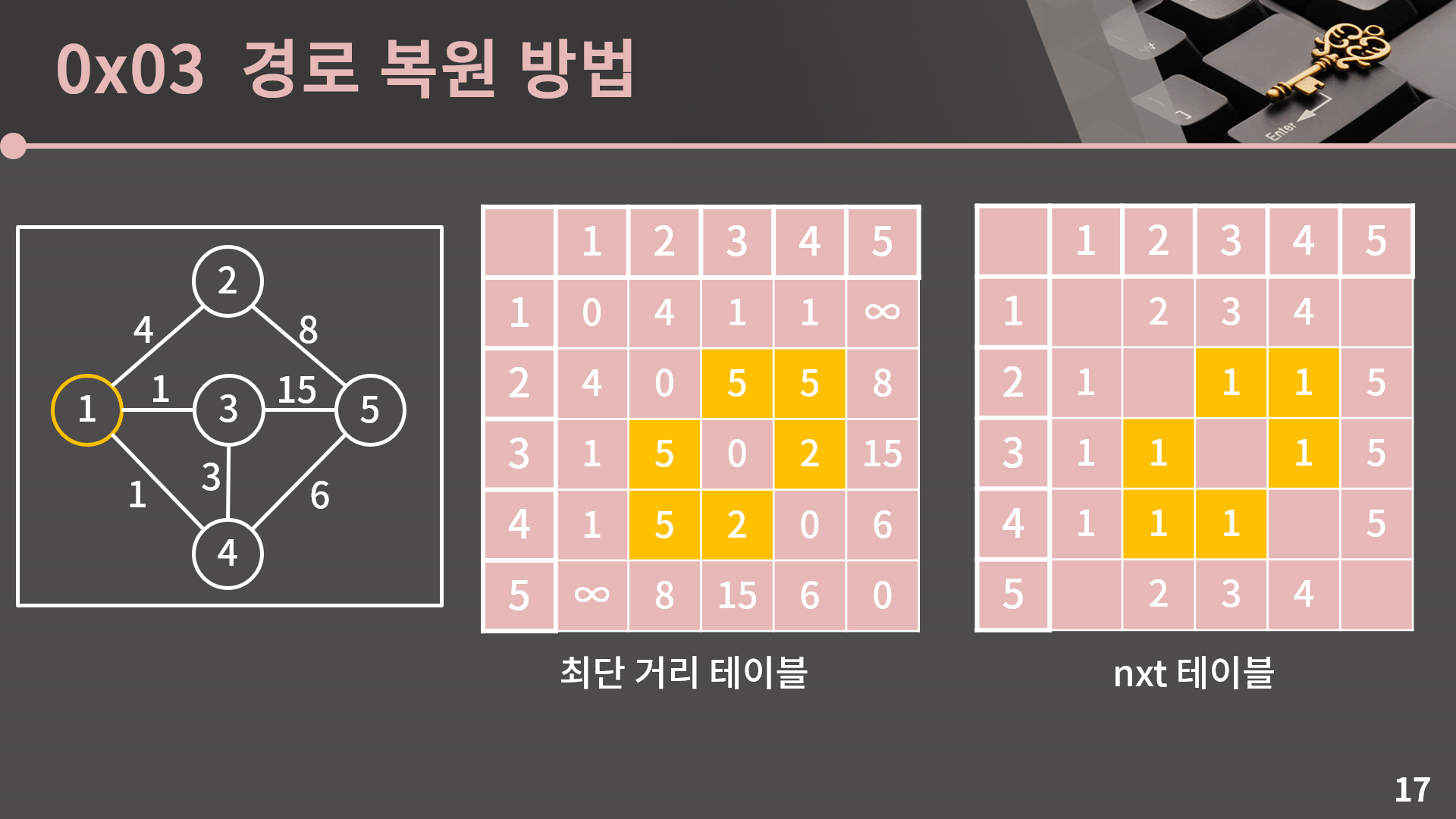
이 다음 단계가 핵심입니다. 맨 처음 최단 거리 테이블은 "중간에 다른 정점을 거치지 않았을 때의 최단 거리"였습니다. 이걸 "중간에 다른 정점을 거치지 않았거나 1번 정점을 거쳐서 갈 때의 최단 거리"가 저장되도록 수정하기 위해 $D[s][t]$보다 $D[s][1] + D[1][t]$가 작을 경우, 즉 1번 정점을 거쳐가는 것이 효율적일 때에만 $D[s][t]$를 $D[s][1] + D[1][t]$로 갱신했습니다.
이 때 $nxt[s][t]$ 또한 갱신을 해주어야 하는데, 기존의 $s$에서 $t$까지 가는 경로보다 $s$에서 1을 먼저 갔다가 1에서 $t$로 가는 경로가 더 효율적인 상황이므로 $nxt[s][t]$를 $nxt[s][1]$ 값으로 대체하면 됩니다. $s$에서 1을 먼저 갔다가 1에서 $t$로 가는 경로가 전체적으로 어떻게 생겼는지는 모르겠지만 일단 $s$에서 1로 가야하는 것은 자명하므로 $s$에서 $t$까지 최단 경로로 가기 위해서는 $s$에서 출발해 $nxt[s][1]$을 가야함을 알 수 있습니다.
최단 거리 테이블에서 $D[2][3], D[2][4], D[3][2], D[3][4], D[4][2], D[4][3]$가 갱신되었으므로 $nxt[2][3], nxt[2][4], nxt[3][2], nxt[3][4], nxt[4][2], nxt[4][3]$ 각각은 $nxt[2][1], nxt[2][1], nxt[3][1], nxt[3][1], nxt[4][1], nxt[4][1]$로 변경됩니다.
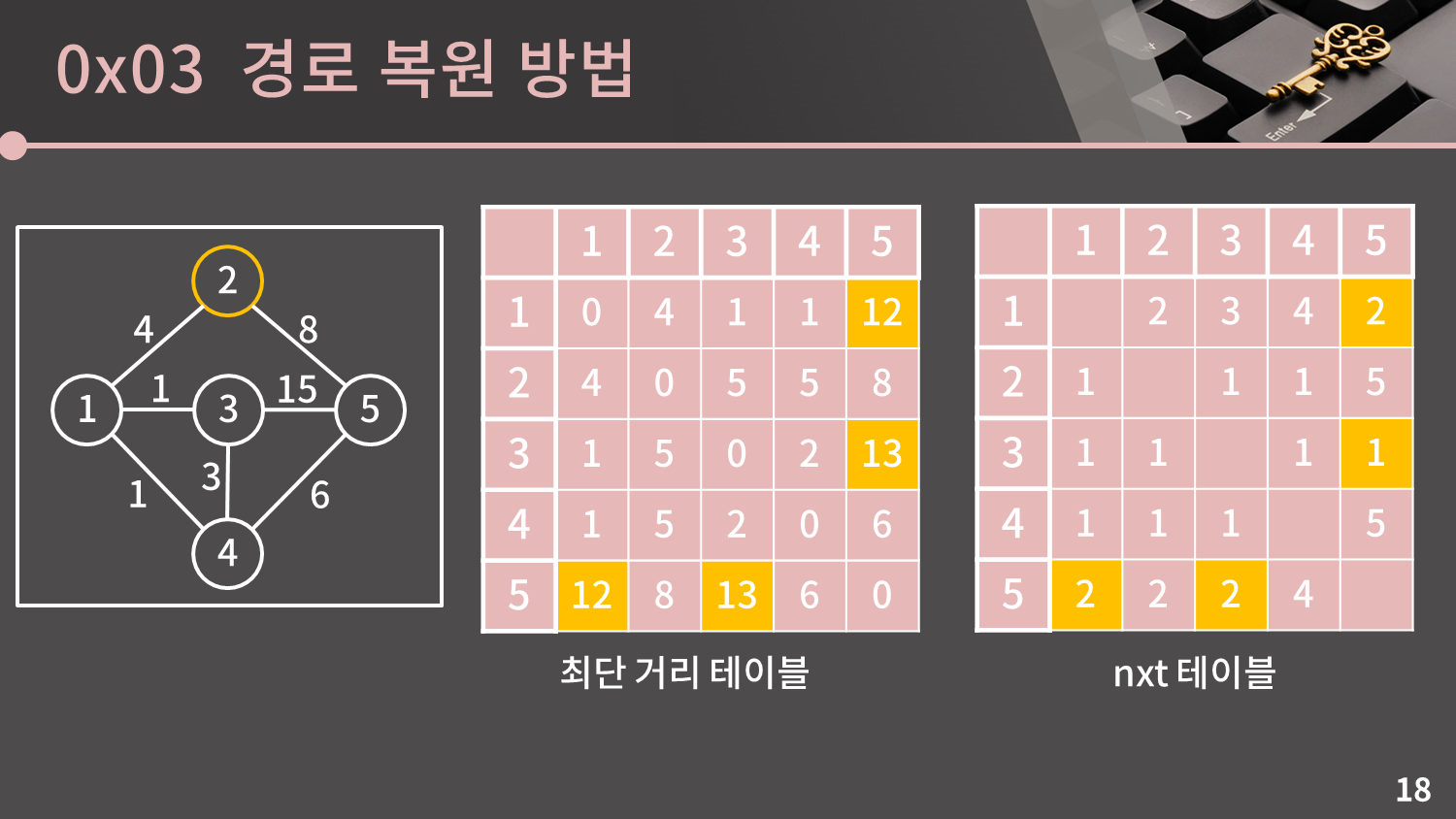
그 다음으로는 2번 정점을 거쳐가는 최단 거리를 따져보아 만약 $D[s][t]$보다 $D[s][2] + D[2][t]$가 작을 경우 $D[s][t]$를 $D[s][2] + D[2][t]$로 갱신합니다.
앞에서 한 것과 마찬가지 논리로 기존의 $s$에서 $t$까지 가는 경로보다 $s$에서 2을 먼저 갔다가 2에서 $t$로 가는 경로가 더 효율적인 상황일 경우 $nxt[s][t]$를 $nxt[s][2]$ 값으로 대체하면 됩니다.
최단 거리 테이블에서 $D[1][5], D[3][5], D[5][1], D[5][3]$이 갱신되었으므로 주어진 테이블에서는 $nxt[1][5], nxt[3][5], nxt[5][1], nxt[5][3]$ 각각은 $nxt[1][2], nxt[3][2], nxt[5][2], nxt[5][2]$로 변경됩니다.
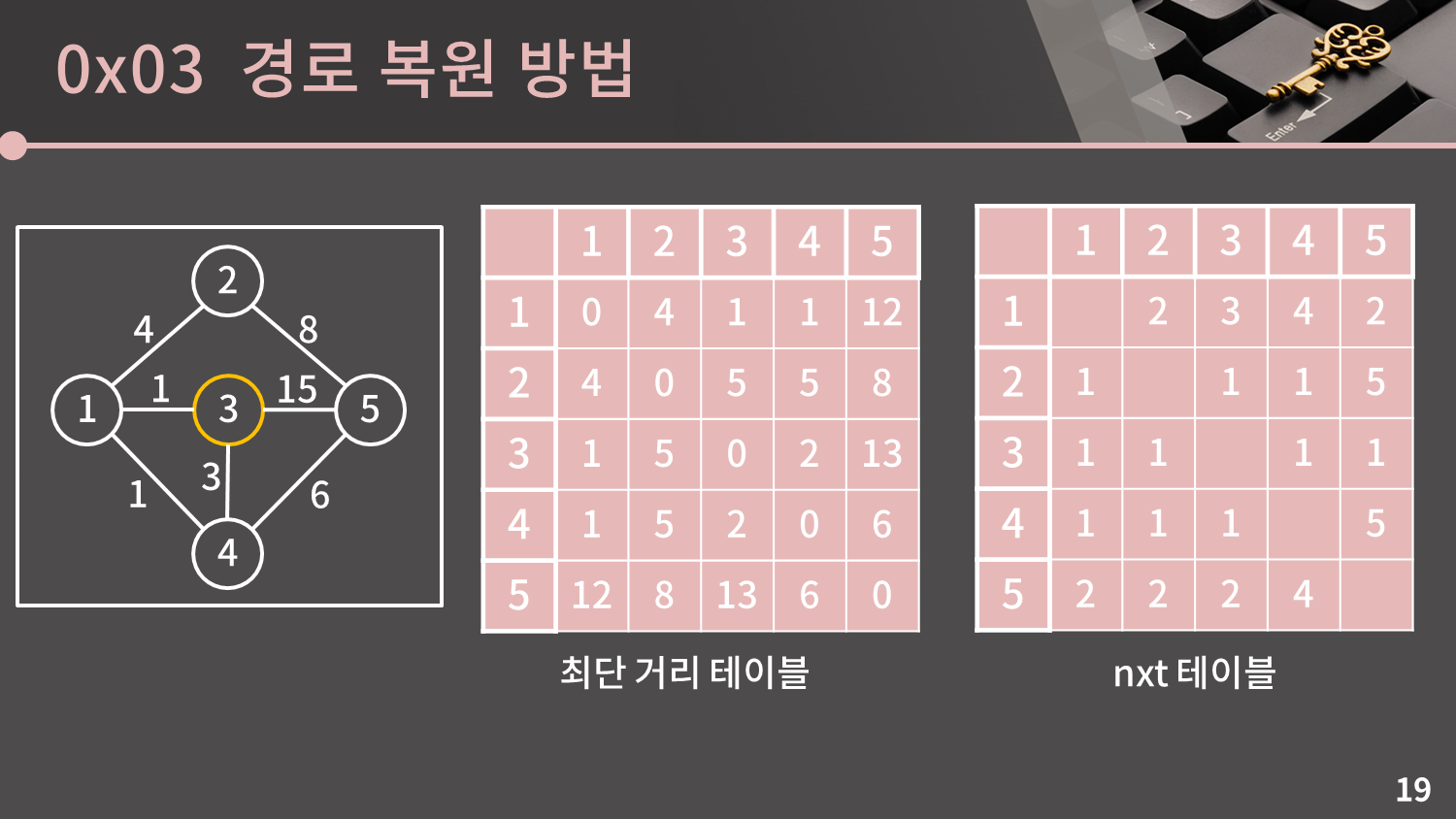
그 다음으로 테이블에 3번을 거쳐가는 최단 거리를 반영하려고 했는데 $D[s][t]$보다 $D[s][3] + D[3][t]$가 작은 경우가 존재하지 않아 아무 일도 일어나지 않습니다.
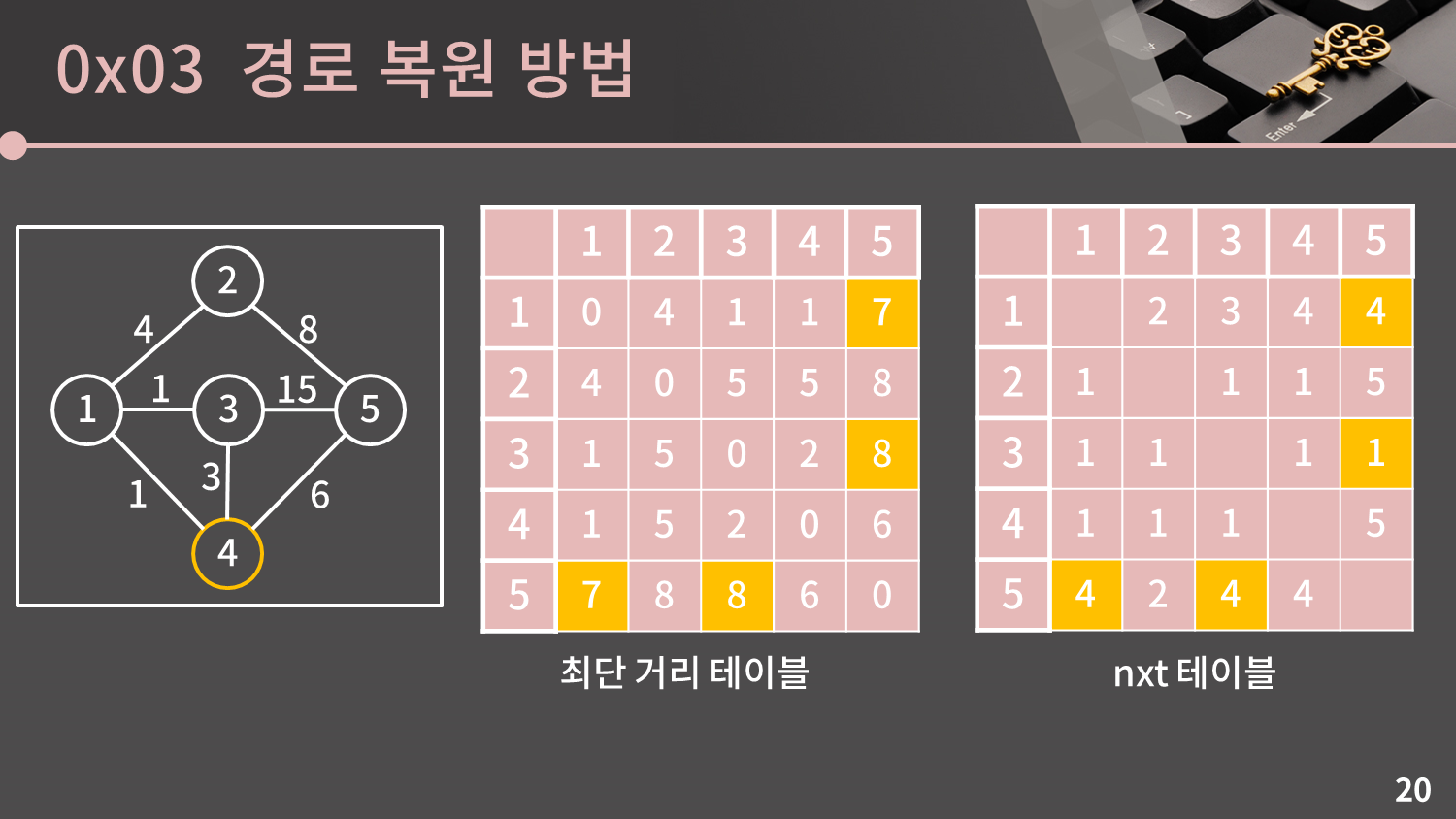
그 다음으로는 4번 정점을 거쳐가는 최단 거리를 따져보아 만약 $D[s][t]$보다 $D[s][4] + D[4][t]$가 작을 경우 $D[s][t]$를 $D[s][4] + D[4][t]$로 갱신합니다.
앞에서 한 것과 마찬가지 논리로 기존의 $s$에서 $t$까지 가는 경로보다 $s$에서 4을 먼저 갔다가 4에서 $t$로 가는 경로가 더 효율적인 상황일 경우 $nxt[s][t]$를 $nxt[s][4]$ 값으로 대체하면 됩니다.
최단 거리 테이블에서 $D[1][5], D[3][5], D[5][1], D[5][3]$이 갱신되었으므로 주어진 테이블에서는 $nxt[1][5], nxt[3][5], nxt[5][1], nxt[5][3]$ 각각은 $nxt[1][4], nxt[3][4], nxt[5][4], nxt[5][4]$로 변경됩니다. 단, 공교롭게도 $nxt[3][5]$의 경우 기존의 값이 1이었는데 $nxt[3][4]$도 1이기 때문에 값이 달라지지 않습니다.
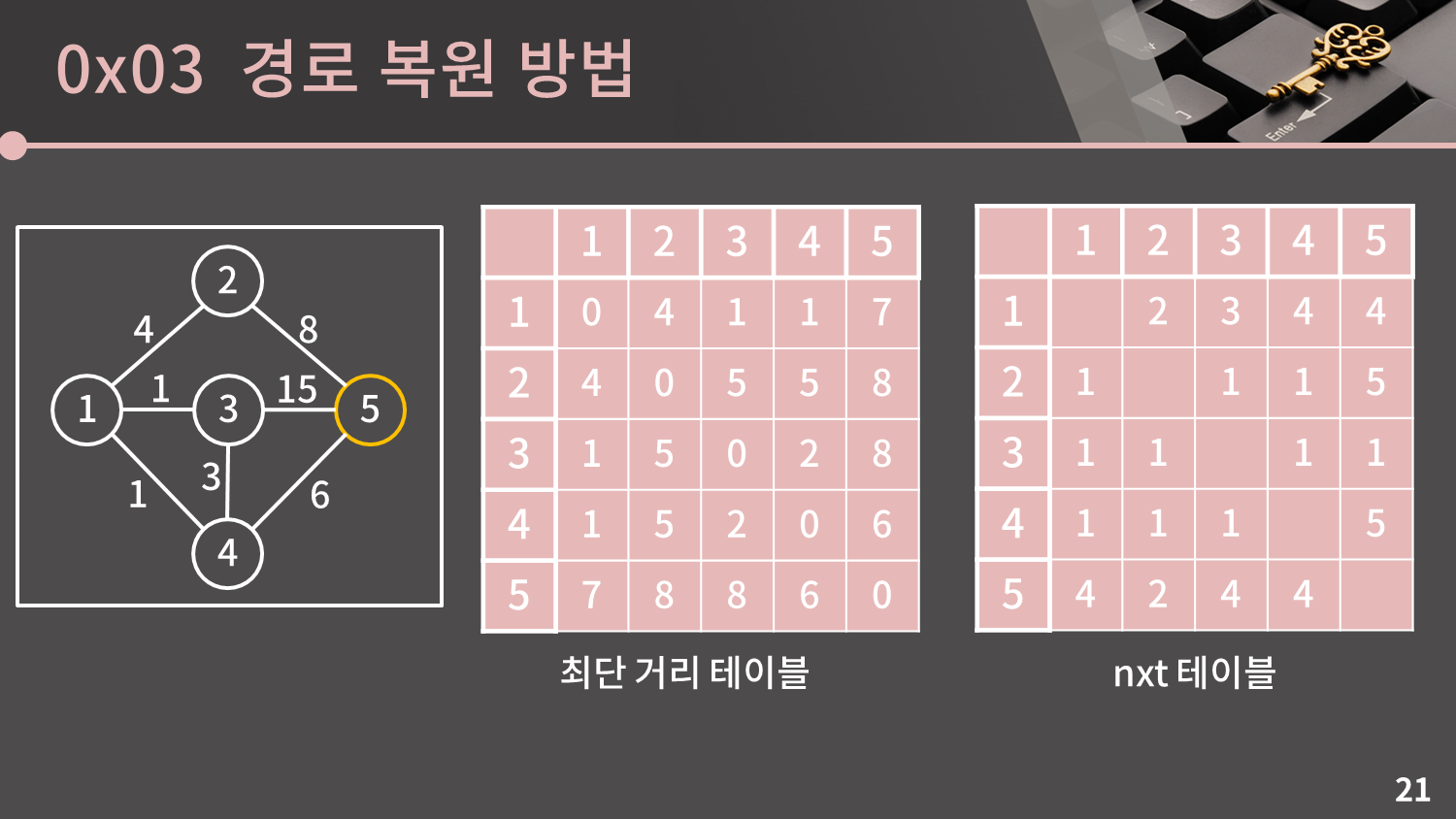
테이블에 5번을 거쳐가는 최단 거리를 반영하려고 했는데 $D[s][t]$보다 $D[s][5] + D[5][t]$가 작은 경우가 존재하지 않아 아무 일도 일어나지 않습니다.

플로이드 알고리즘이 종료되었고 이번에는 최단 거리 테이블뿐만 아니라 $nxt$ 테이블까지 얻었습니다. 이를 통해 어떻게 경로 복원을 할 수 있을까요?
3에서 5까지 가는 경로를 복원해봅시다. 이 예제만 보고나면 바로 이해가 갈 것입니다.
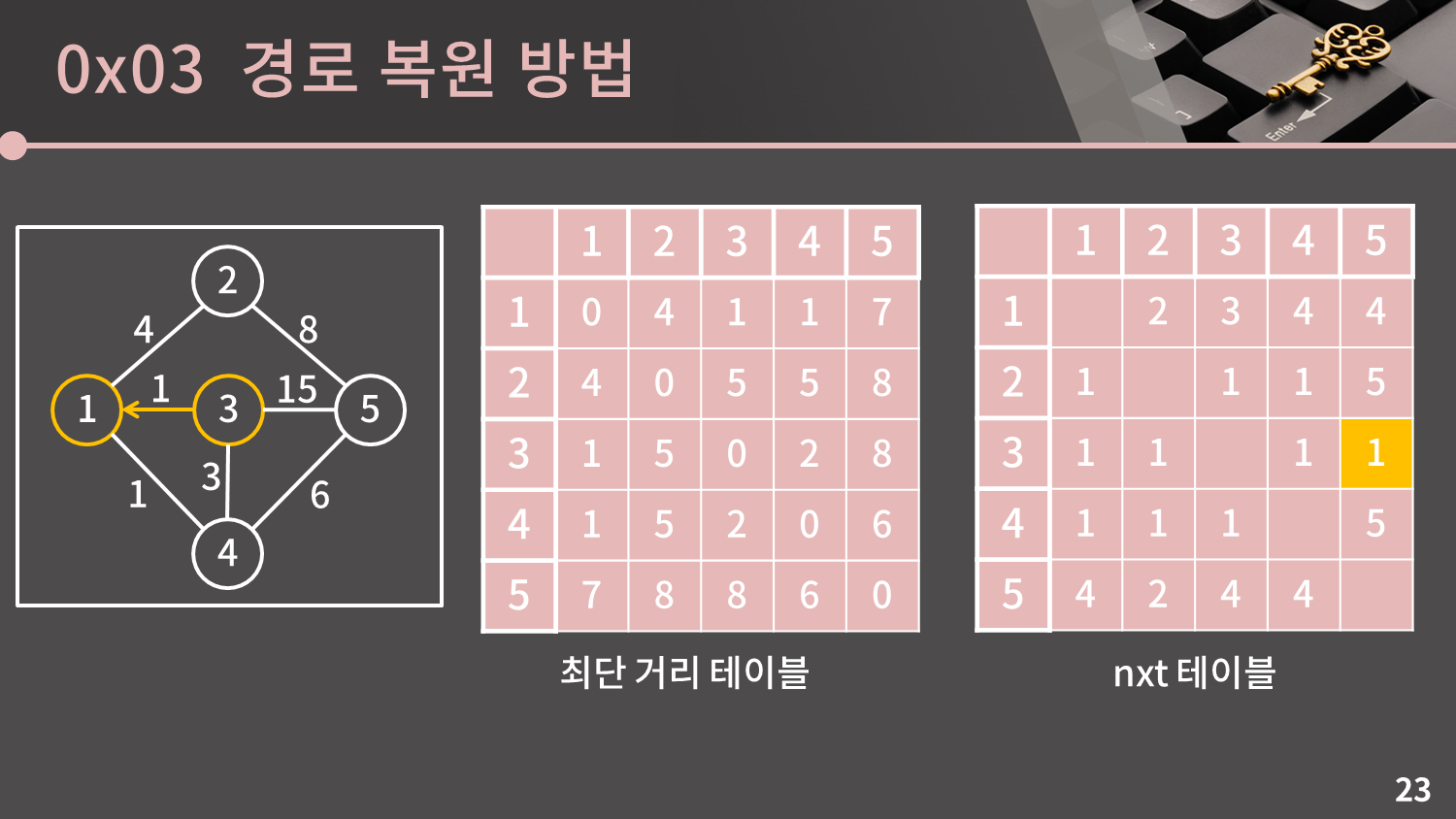
딴건 모르겠고 $nxt[3][5]$가 1이므로 일단 3에서 1로 갑니다.
그 다음은 어디로 가야할까요?

현재 1에 와있으니 1에서 5까지 최단 거리로 가면 될 것입니다. $nxt[1][5]$가 4이므로 1에서 4로 갑니다.
그 다음은 어디로 가야할까요?
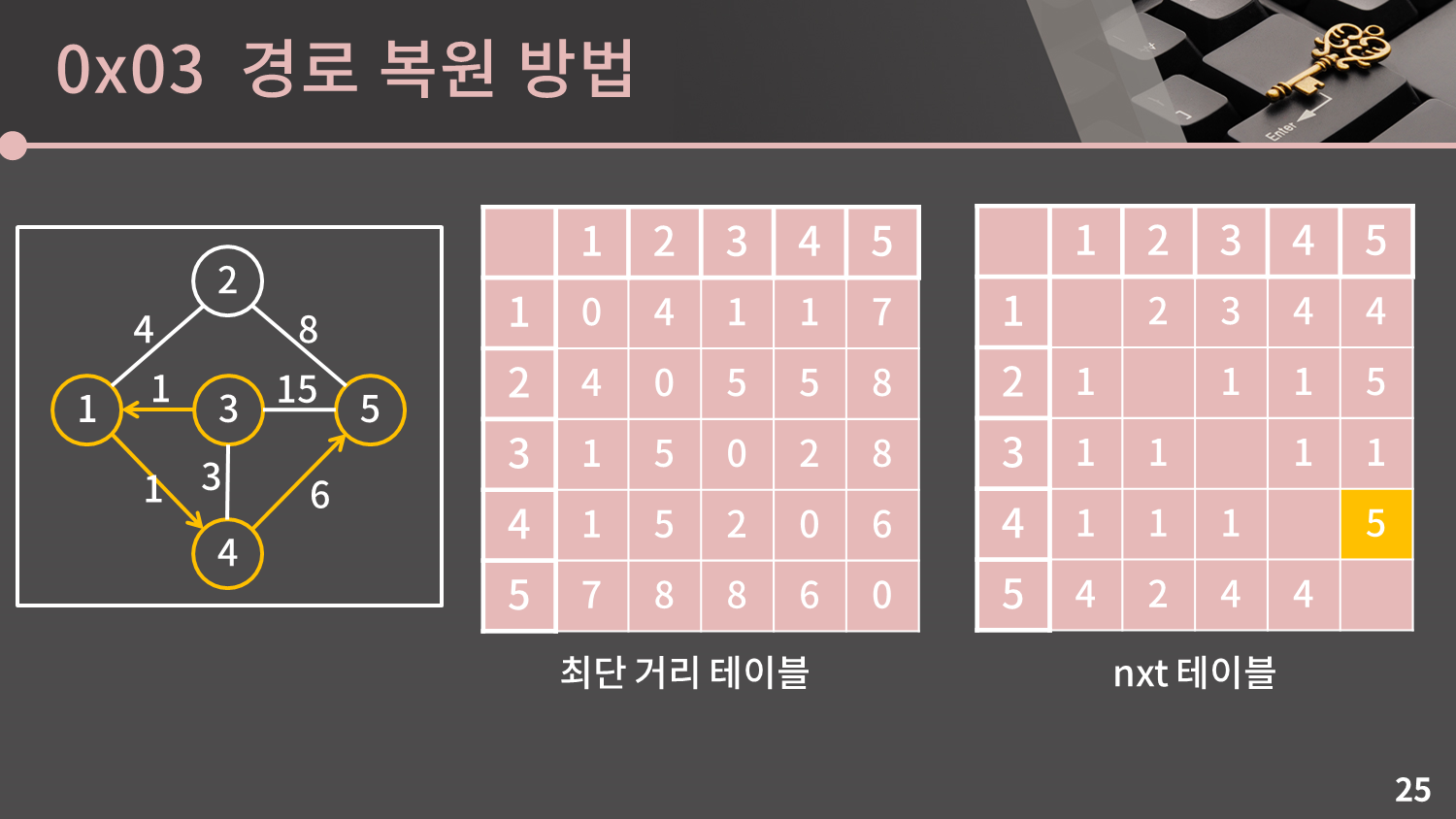
현재 4에 와있으니 4에서 5까지 최단 거리로 가면 될 것입니다. $nxt[4][5]$가 5이므로 4에서 5로 갑니다.
축하합니다. 목적지에 도착했습니다. 이와 같이 $nxt$ 테이블을 이용해 한 단계씩 앞으로 전진하면 경로를 복원해낼 수 있습니다.

지금까지 공부를 착실하게 해왔다면 $nxt$ 테이블이 주어졌을 때 $s$에서 $t$로 가는 경로를 복원하는 것을 어렵지 않게 구현할 수 있을 것입니다. $cur$ 변수가 $s$에서 시작해 $t$까지 가는 동안 $nxt$를 계속 타고 가며 $path$ vector에 계속 push_back을 해주면 됩니다.

그 다음으로 풀어 볼 문제는 BOJ 11780번: 플로이드 2 문제입니다. 이 문제에서는 최단 거리와 더불어 경로까지 출력할 것을 요구합니다.
이전 문제에 썼던 코드에서 $nxt$ 배열을 갱신하고, 이후 $nxt$ 배열을 이용해 경로를 출력할 수 있도록 수정을 하면 됩니다. 정답 코드를 확인하기 전 꼭 직접 한 번 시도해보세요.

대부분의 코드가 유사하니 $nxt$배열과 관련한 부분만 짚고 넘어가겠습니다. 우선 15~20번 줄에서 입력을 처리하는데, 이 때 19번째 줄과 같이 $nxt$ 배열의 값도 변경을 시킵니다. 그리고 23~29번 줄에서 $d$ 테이블을 갱신할 때 27번째 줄의 처리가 들어갑니다.

37~54번 줄은 경로를 출력하는 구간입니다. $nxt$ 테이블을 이용해 경로를 적절하게 복원해주면 됩니다.

이번 강의를 통해 플로이드 알고리즘을 익혔습니다. 플로이드 알고리즘은 무방향 혹은 방향 그래프에서 모든 정점 쌍 사이의 최단 거리와 그 경로를 $O(V^3)$에 알아낼 수 있는 알고리즘입니다. 만약 주어진 문제가 모든 정점 쌍 사이의 최단 경로를 구하도록 요구하는 문제이면 플로이드 알고리즘이 정해일 확률이 높습니다. $O(V^3)$이라는 시간복잡도가 굉장히 크게 느껴질 수 있지만 간선이 매우 적을 때에만(=간선은 최대 $V^2$개 정도인데 $V$개에 가까울 때만) 다음 강에서 배울 다익스트라를 $V$번 돌리거나 Johnson's algorithm을 사용해 $O(V^2logV + VE)$에 모든 정점 쌍 사이의 최단 거리를 구할 수 있습니다. 간선이 $V^2$개에 가까울 경우 플로이드보다 더 효율적인 알고리즘은 존재하지 않습니다.
또한 플로이드 알고리즘은 단순 덧셈 계산 후 비교와 대입만으로 이루어져있기 때문에 $V$가 1000정도 되어 $V^3$이 10억 가까이 되는 상황이라고 하더라도 1초 내외에 알고리즘이 종료될 정도로 아주 빠르게 동작하니 이를 감안해 풀이를 생각해보면 되겠습니다.
연습 문제 열심히 푸세요!
'강좌 > 실전 알고리즘' 카테고리의 다른 글
| [실전 알고리즘] 0x00강 - 오리엔테이션 (49) | 2020.02.10 |
|---|---|
| 실전 알고리즘 강좌 리뉴얼에 대한 안내 (29) | 2020.01.29 |
| [실전 알고리즘] 0x14강 - 다익스트라 알고리즘_구버전 (24) | 2020.01.29 |
| [실전 알고리즘] 0x12강 - 최소 신장 트리_구버전 (18) | 2020.01.27 |
| [실전 알고리즘] 0x11강 - 위상 정렬_구버전 (13) | 2020.01.17 |
| [실전 알고리즘] 0x10강 - 트리_구버전 (16) | 2019.12.28 |